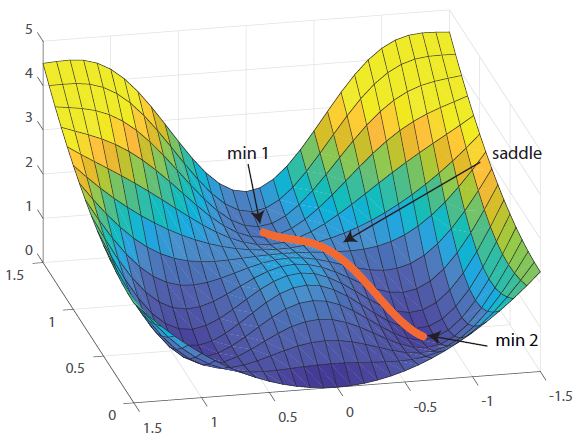
The Hydra String Method
The Hydra String Method (HSM), is an extension of the String Method and the Climbing String Method given by Vanden Eijnden. The HSM uses the eponymous "string" to climb up to a saddle point of a surface. The string then finds a connected minimum and, from this minimum, more climbing strings spring out to find more saddles. Like a Hydra, the string grows new heads and explores the surface. The HSM also returns the minimum energy paths (MEPs) between local minima. That is, the paths that require the least "upward" movement.
One of the major benefits of the HSM is its high degree of parallelizability. There are multiple aspects of the algorithm that can be paralellized but, generally, only one aspect can be parallelized at a time. The computations consist of relatively simple algebra, but the computational load is much larger than the memory transference overhead making the HSM an excellent candidate for GPU implementation.
Using the HSM, I have been able to explore the PES of two-dimensional granular systems and describe interesting features about the complicated structure therein. Viewing the PES as a network of minima connected with saddle points allows me to utilize graph theoretical approach. Metrics such as betweenness centrality, clustering coefficient, and geodesic distance can help to illuminate the system's dynamics.